Transzformációk, függvénytulajdonságok – Óraterv

Hekkelné Zsiros Ildikó küldte be time időpontban
PDF
Terv típusa
Óraterv
Szektor
Természettudományok, matematika és statisztika
Témakör, tanulási terület
Trigonometria
Szakmai tantárgy(ak)
Matematika
Évfolyam
11. évfolyam
Fejlesztendő kompetenciák, készségek
IKT (információ, kommunikáció, technológia)
Kommunikáció és együttműködés
Kreativitás és innováció
Kritikus gondolkodás és problémamegoldás
Fejlesztendő szakmai kompetenciák, készségek
− Felidézés, koncentrációs, megfigyelő képesség fejlesztése. − Lépésekre bontás, rendszerezés (táblázat). − A feladatmegoldó képesség. − Szintetizálás képessége. − Geometriai látásmód, összefüggés a témakörök között. − Esztétikai érzék fejlesz
Módszer, tanulásszervezési
szemléltetés
szimuláció
Közoktatási tantárgy(ak)
matematika
Tanulási, fejlesztési célok
− Röpdolgozat eredmények megbeszélése. Az értékelés célja a tanulók fejlődésének segítése. − A függvénytani ismeretek felelevenítése, aktivizálása, az új ismeretek egy rendszerbe foglalása, gyakorlás, elmélyítés. −Alkalmazás a trigonometrikus függvényekre
Fogalmak
Függvénytranszformációk, függvénytulajdonságok
Szükséges eszközök
Számológép, táblafilc, iratlefűző tasak, nyomtatott trigonometrikus koordináta-rendszer. Kókuszrúd, csomagolópapír, vágóeszköz
Időtartam
45 perc
Az óra / projekt bevezető része, előkészítése

Röpdolgozatok kiosztása, értékelése. (Értékelés, visszajelzés, megerősítés.)

5' Házi feladat ellenőrzése, összefüggések megállapítása: 
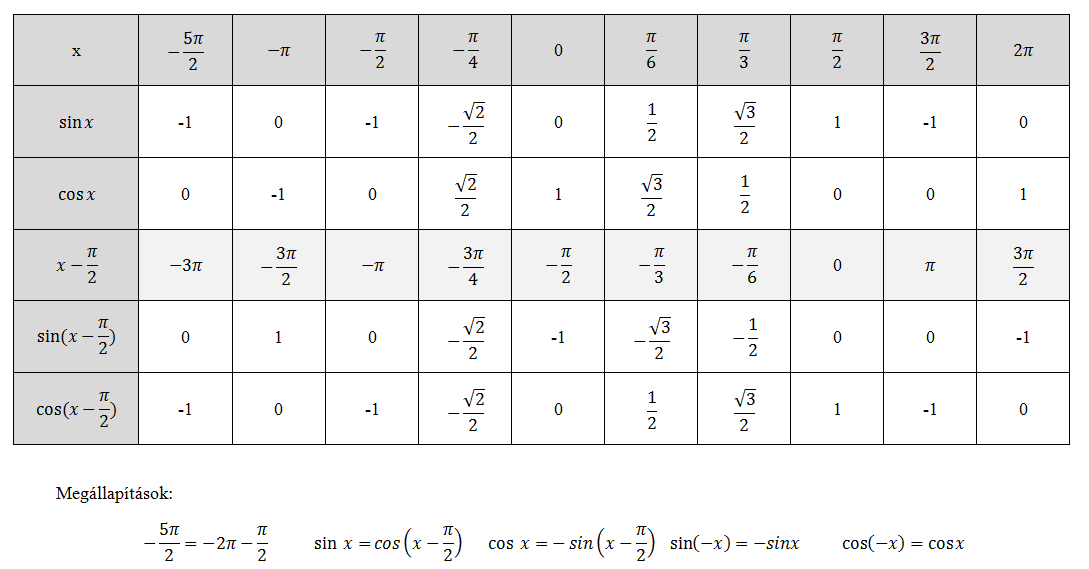
 (Tk 121.oldal Hf. 3.) A feladathoz tartozó táblázat kivetítése. 
Megállapítások:
1) A sin x fgv, grafikonja a cos x fgv. grafikonjából egy x tengely irányú – vel való eltolással áll elő.
2) A cos x fgv, grafikonja a sin x fgv. grafikonjából egy x tengely irányú – vel való eltolással és egy x tengelyre vonatkozó tükrözéssel áll elő.

Hf.

 

Az óra / projekt megvalósítása

6' Függvényábrázolás és jellemezés

  1. példa: fgv
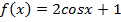
    Függvény zérushelyének meghatározása algebrai úton az  f (x) = 0 egyenlet megoldásával: 

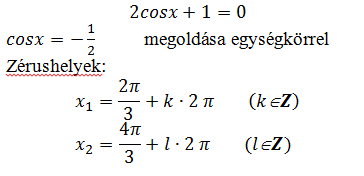
    fgv.ábrázolás

5' Függvény transzformációk csoportosítása, rendszerező áttekintése 
Részösszefoglalás: Az ismeretek rendszerezése és rögzítése táblázatban.
Párok összegyűjtik az ismereteket.  Kitöltendő táblázat kivetítése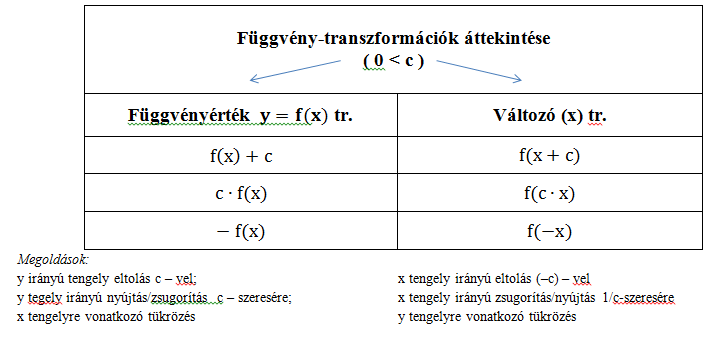

5' Zanza Tv videó: Periodikus függvények transzformálása
https://zanza.tv/matematika/osszefuggesek-fuggvenyek-sorozatok/periodikus-fuggvenyek-transzformalasa
Tantárgyközi kapcsolatok: fizika, hanghullámok, oszcilloszkóp
oszcilloszkóp

10' Függvényábrázolás gyakorlása
Ábrázoljuk fólián táblafilccel a megadott függvényeket!
(Páros munka: megbeszélik a transzformációs lépéseket.
Kooperáció fejlesztése. Egymás munkája iránti felelősség, önellenőrzés. 
A páros tagjai segítik egymást a tanulásban.)
(Eszközök: Lefűzhető fóliatasak, bele sablon koordináta-rendszer trigonometrikus függvény ábrázolásához, táblafilc, törlőkendő.)
Nevezzük meg azokat a függvény tulajdonságokat, amelyek a transzformáció hatására megváltoztak!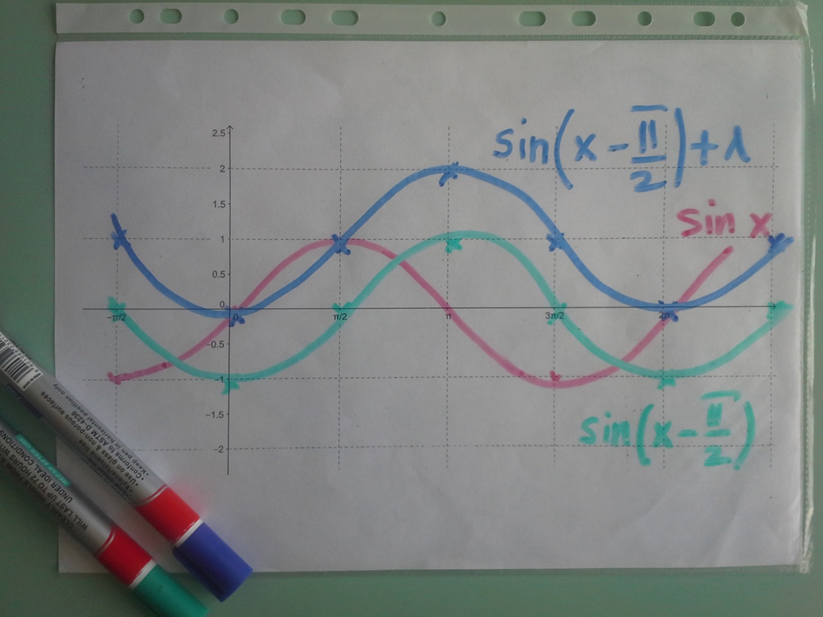

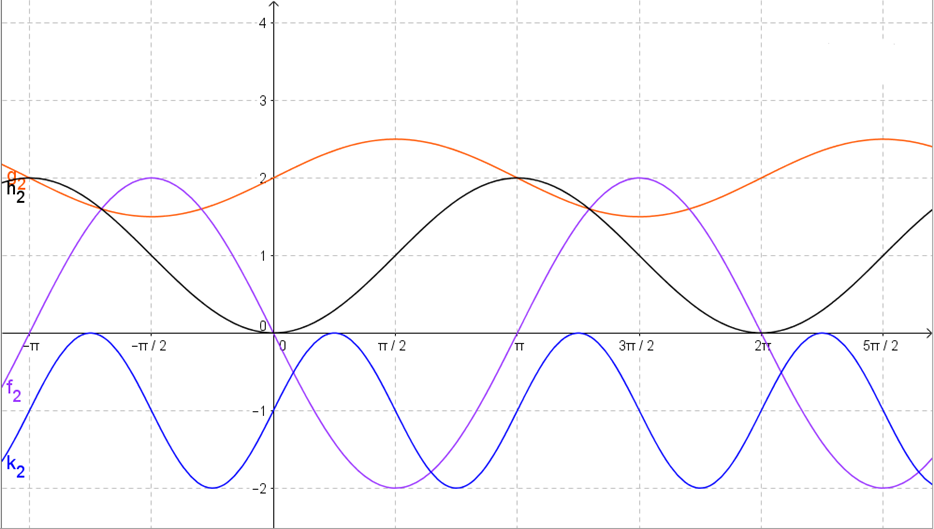
Ellenőrzés: GeoGebra programmal kivetítve.


5' RÁADÁS:
- Csavarjunk be egy szál kókuszrudat  egy írólapba, majd vágjuk el egy, a hengert 45°-os szögben metsző síkkal (késsel)!
- Terítsük ki a síkba a csomagolópapírt, a henger palástját!
- Milyen görbe lett a határoló vonala?

Szorgalmi feladat:
Próbálj kapcsolatot keresni:
1. Mekkora a henger átmérője, mekkora a sugara?
2. Hogyan lehetne ferdébben elvágott hengerhez jutni?

Tananyag készítéséhez használt alkalmazás
Geogebra
Értékelési terv

A tanár a fóliára felrajzolt függvényeket ellenőrzi munka közben.
A tanóra végén az órai munka, aktivitás értékelése jeggyel.

Differenciálás

Egyéni munka: mindenki a saját fóliáján ábrázolja a függvényt.
A tanár a fóliára felrajzolt függvényeket ellenőrzi munka közben.
Segítségnyújtás.

 

Házi feladat, projektfeladat

A tanórához kapcsolódó házi feladat kijelölése:

Tk. 123.oldal Hf. 1.) - 3.)-ig feladatai

A házi feladat megoldására való felkészítés.