Ni posebnih gradiv izdelanih pred poukom.
Okviren čas uvodnega dela učne ure je predviden na 7 minut.
Z dijaki ponovimo učno snov, ki smo jo obravnavali v preteklih nekaj urah in sicer ponovimo, da ničle polinoma iščemo ali s pomočjo razstavljanja ali pa s celoštevilskimi kandidati, ki jih preverjamo s Hornerjevim algoritmom. Z dijaki skupaj (vodeno s strani učitelja) povzamemo, da se nekatera števila lahko večkrat pojavijo kot ničle polinoma.
Dijaki aktivno sodelujejo pri odgovorih in podajajo pripombe pri vodenem ponavljanju učne snovi. Zastavljajo vprašanja in brskajo po zapiskih, ki jih imajo v zvezkih iz preteklih učnih ur. Učitelj jih spodbuja, da se poslužijo svojih zapiskov kot pomoč pri ponovitvi oz. iskanju odgovorov.
Okviren čas izvajanja dela učne ure je predviden na 35 minut.
- Na tablo zapišemo novo poglavje in sicer graf polinoma.
- Poleg definicije grafa polinoma z dijaki dorečemo, da bomo za najboljši približek risanja grafa polinoma potrebovali tri stvari:
- Ničle polinoma.
- Začetno vrednost.
- Obnašanje polinoma v obeh neskončnostih oz. daleč stran od njegovih ničel.
- Preden začnemo s konkretnim risanjem na računalniku zaženemo spletni program https://www.geogebra.org/classic?lang=en
- Prižgemo šolski projektor, ki prikazuje pogled na okolje Geogebra in v programu nastavimo in popravimo pogled, da je spremljanje lažje.
- S pomočjo Geogebre narišemo sledeče grafe polinomov:
- p(x)=(x-1)(x-2)(x-3)
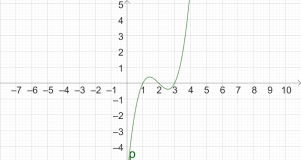
- p(x)=(x-1)^2 (x-2) (x-3)^2
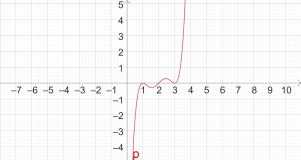
- p(x)=(x-1)^3 (x-2)^2 (x-3)
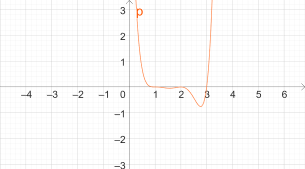
- p(x)=(x-1)^4 (x-2)^2 (x-3)^3
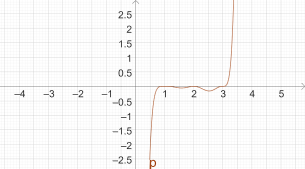
- p(x)=(x-1)(x-2)(x-3)
- Pri posamezni primerih dijake spodbujamo, da si zabeležijo obnašanje grafa v okolici ničel in da iz danih primerov poskušajo zapisati pravilo oz. poskušajo induktivno sklepati in zapisati splošno pravilo za obnašanje grafa v okolici ničel polinoma.
- Povzamemo njihove ugotovitve, jih natančneje opredelimo in ustrezno zapišemo z matematičnimi simboli.
Vrednotenje razumevanja obravnavane učne snovi izvedemo pri naslednjih učnih urah in sicer pri pregledu opravljenih domačih nalog in pri spremljanju risanja grafov polinomov dijakov pri pouku po tem, ko z dijaki premislimo še drugi dve točki (2. začetna vrednost polinoma in 3. obnašanje polinoma v obeh neskončnostih oz. daleč stran od njegovih ničel).
/
/
